Calculate a definite integral for a function in Spectrum BASIC

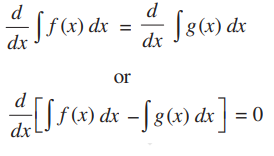
What is and how to calculate a definite integral for a function?

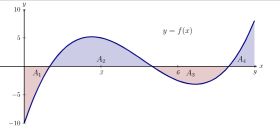
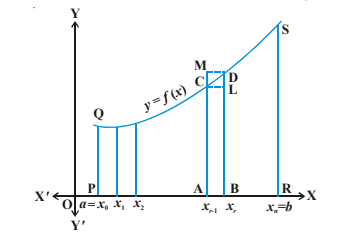
Calculating a definite integral involves finding the area under a curve between two given limits. There are several methods to calculate definite integrals, and I’ll explain two commonly used techniques: the Riemann sum approximation and the fundamental theorem of calculus.

Riemann Sum Approximation:

Divide the interval of integration [a, b] into smaller subintervals.
Choose a representative point (usually the left endpoint, right endpoint, or midpoint) within each subinterval.
Evaluate the function at each representative point to get the corresponding function values.
Multiply each function value by the width of the subinterval.
Sum up all the products to approximate the area under the curve.
As the number of subintervals increases, the approximation gets closer to the actual value of the definite integral.

Fundamental Theorem of Calculus:

If F(x) is the antiderivative (indefinite integral) of the function f(x), then the definite integral of f(x) from a to b is equal to F(b) – F(a).
Find the antiderivative F(x) of the given function f(x).
Evaluate F(x) at the upper limit b and subtract the value of F(x) at the lower limit a.
For more complex functions where finding an antiderivative is not feasible, numerical methods like Simpson’s rule, trapezoidal rule, or numerical integration techniques (e.g., Gaussian quadrature) can be employed to approximate the definite integral.

It’s worth noting that calculators, mathematical software (such as MATLAB or Python libraries like SciPy), and online integral calculators can also provide numerical approximations of definite integrals for a wide range of functions.

Remember to choose the appropriate method based on the complexity of the function and the required accuracy of the result.

How to write a program in Spectrum BASIC to calculate a definite integral for a function?

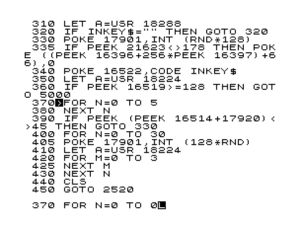
ZX Spectrum Basic does not have built-in functions or commands specifically designed for numerical integration or calculating definite integrals. However, you can implement a basic numerical integration algorithm, such as the Riemann sum method, to approximate the definite integral of a function. Here’s an example ZX Spectrum Basic program that demonstrates this approach:

10 PRINT “Definite Integral Approximation”
20 PRINT “Enter the limits of integration:”
30 INPUT “Lower limit (a): “, a
40 INPUT “Upper limit (b): “, b
50 INPUT “Number of subintervals: “, n
60 LET dx = (b – a) / n
70 LET sum = 0
80 FOR i = 0 TO n – 1
90 LET x = a + i * dx
100 LET y = YOUR_FUNCTION(x)
110 LET sum = sum + y * dx
120 NEXT i
130 PRINT “Approximation of the definite integral: “; sum
140 PRINT “End of program”

In this program, you need to replace YOUR_FUNCTION with the function you want to integrate. Make sure to define your function as a ZX Spectrum Basic expression that takes the input x and returns the corresponding function value y. For example, if you want to integrate the function f(x) = x^2, you would replace YOUR_FUNCTION with x * x in line 100.

The program prompts you to input the lower limit (a), upper limit (b), and the number of subintervals (n) for the numerical integration. It then calculates the width of each subinterval (dx) and initializes the sum variable to 0.

The loop iterates through each subinterval, calculating the representative x-value (line 90), evaluating the function at that point (line 100), and adding the product of the function value and the width of the subinterval to the sum variable (line 110).

Finally, the program prints the approximation of the definite integral (line 130) and displays “End of program” to indicate the completion of the execution.

Note that this method provides an approximation of the definite integral and the accuracy will depend on the number of subintervals chosen. Increasing the value of n will generally improve the approximation.

Remember to adapt the program and input the appropriate function according to your specific integration problem.